为什么探头晶片的厚度要设计为二分之一波长（λ/2）或者是（λ/2）的奇数倍？

我们知道超声波的发射是通过激励电压迫使探头晶片做厚度方向振动产生的。

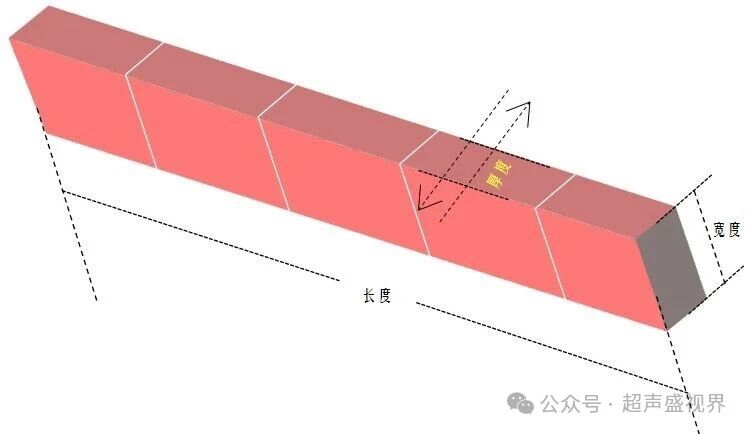
压电晶片的厚度也不是随意决定的。其厚度须满足二分之一波长（λ/2）或者是（λ/2）的奇数倍？

为什么这样做：

其根本目的是为了实现压电晶片的共振，从而最大限度地提高超声波的发射和接收效率。

超声探头的核心是压电晶片。当交变电场加在晶片两端时，晶片会因压电效应而发生厚度方向的伸缩振动。这种振动在晶片内部向前后两个表面传播，并在表面发生反射。

压电晶片的两个表面是声阻抗突变的界面（从晶片到匹配层或背衬）。前界面：压电晶片到匹配层，后界面：压电晶片到背衬阻尼。

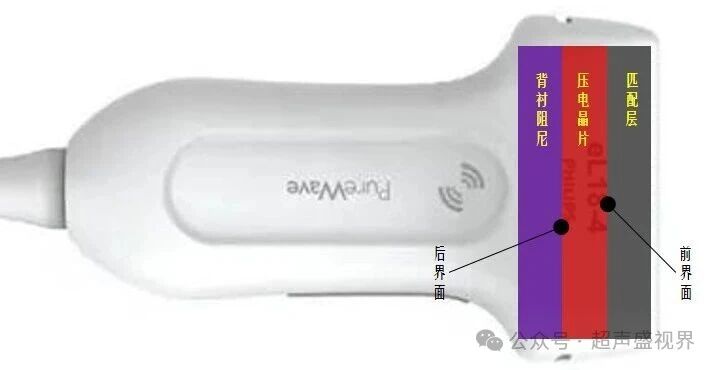
当晶片的厚度（d） 恰好等于超声波在压电晶片材料中的波长 （λ） 的一半时，即 d = λ/2，就会满足一个完美的共振条件。

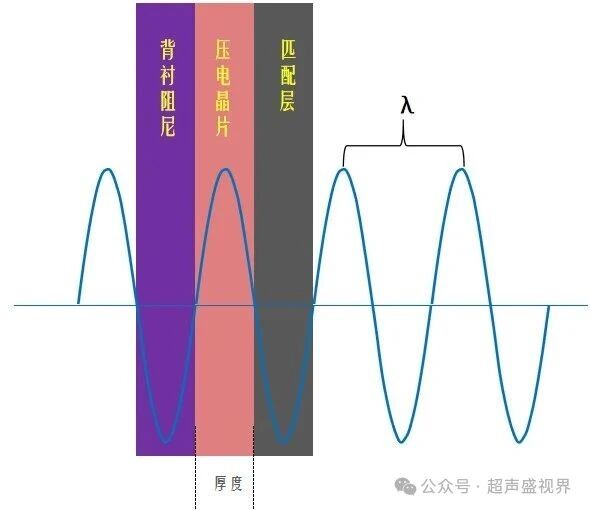
当它工作时，超声波沿厚度方向传播，到达表面时，除非与其接触的介质的声阻抗与其完全相同,否则就会有反射波被反射回来，如下图，前、后界面的反射波与入射波的相位均发生了180度的反转，造成峰-峰相遇或者是谷-谷相遇，根据波的干涉原理，峰-峰相遇或者是谷-谷相遇时，振动加强，振幅最大。

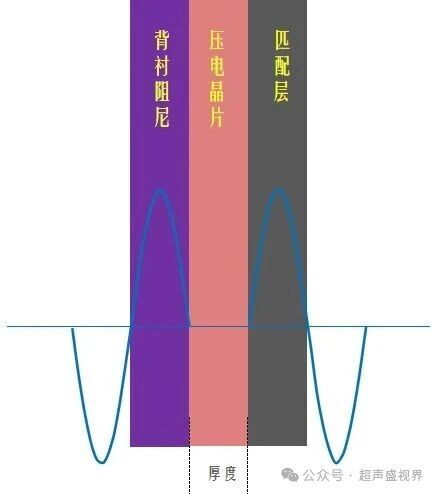
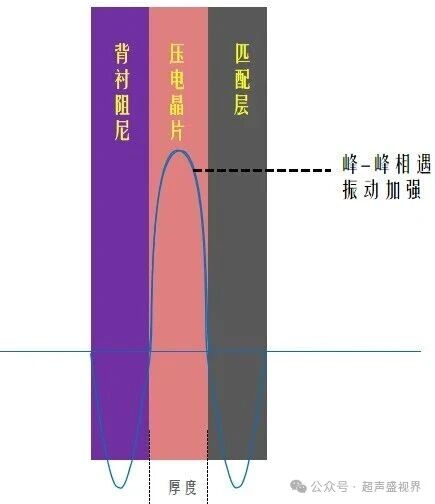
因此

压电元件的厚度恰好等于半个波长（λ/2）时,或者说（λ/2）的奇数倍时,两个方向的超声波同相,振动加强,这叫谐振，该波长对应的频率,叫基本谐振频率,厚度为（λ/2）的奇数倍,也发生谐振,称为高次谐振，对应的频率称为高次谐振频率(3次谐振频率、5次谐振频率等),

当压电元件的厚度为（λ/2）的偶数倍时，例如压电晶片的厚度等于波长，两个方向的波反相,相互抵消,振动最弱。

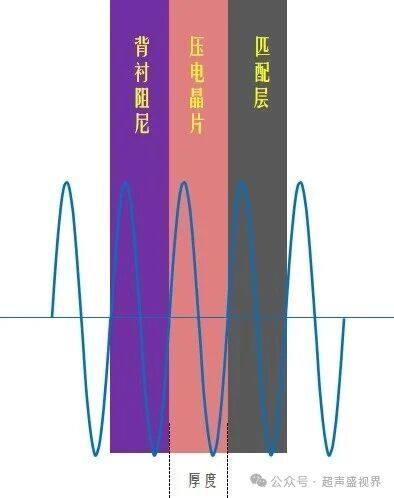
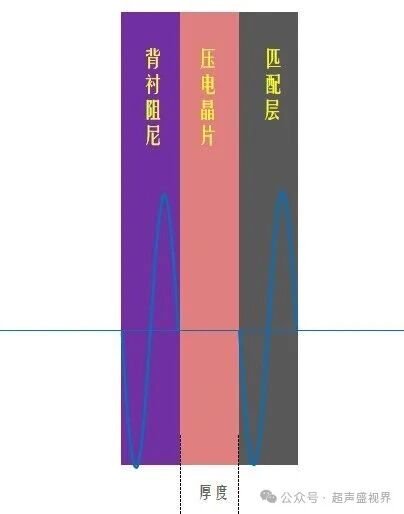
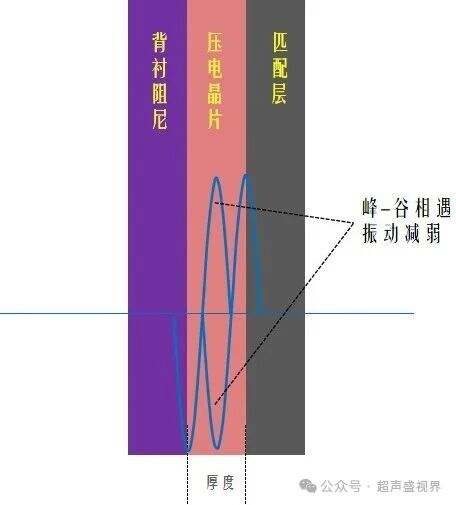
为什么共振如此重要？—— 效率最大化
共振带来的好处是巨大的：

发射效率最高：在共振频率下，只需要一个相对较小的交变电压，就能驱动晶片产生最大幅度的机械振动。这就好比轻轻一推就能让秋千荡得很高。这意味着电能到声能（机械能）的转换效率最高，探头能发射出能量最强的超声波。

接收灵敏度最高：同理，当非常微弱的外部超声波信号（回声）作用在晶片上时，如果其频率等于晶片的共振频率，就会引发晶片最强烈的振动，从而产生最强的电信号。这大大提高了探头接收微弱回声的灵敏度。

频率确定且纯净：共振使得探头主要在其基频（由厚度决定的主频率）附近工作，产生的超声波频率单一、纯净，这对于获得高分辨率的超声图像至关重要。

简单来说，将晶片厚度设计为λ/2，就是把它“调谐”到了一个特定的频率上，在这个频率下，它既能最卖力地“喊”（发射），也能最灵敏地“听”（接收）。

波长（λ）是如何确定的？
这里有一个关键点：公式d = λ/2 中的波长 λ，指的是超声波在压电晶片材料本身中的波长，而不是在人体组织或水中的波长。

波长的计算公式是：
λ = c / f
其中：

c 是声波在压电晶片材料中的声速（单位：m/s）。

f 是我们希望探头工作的中心频率（单位：MHz）。

因此，当工程师要设计一个中心频率为f 的探头时，他们会：

选定一种压电材料（如PZT，已知其声速c）。

计算出在该材料中的波长λ = c / f。

将晶片的厚度加工成d = λ/2。

举例：

假设用PZT材料（声速 c ≈ 4000 m/s）制作一个5 MHz的探头。

波长λ = c / f = 4000 m/s / 5,000,000 Hz = 0.8 mm。

晶片理想厚度d = λ / 2 = 0.4 mm。

实际应用中的细微考量：
在实际生产中，情况会稍微复杂一点：

λ/2的倍数：理论上，厚度为 λ/2的奇数倍（如λ/2， 3λ/2， 5λ/2 ...）都能实现共振。但最常用、最基础、性能最好的是基频模式（λ/2）。更厚的晶片（如3λ/2）虽然也能共振，但会使探头变得笨重，且振动模式可能更复杂。